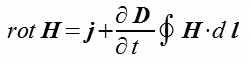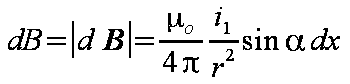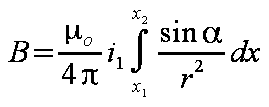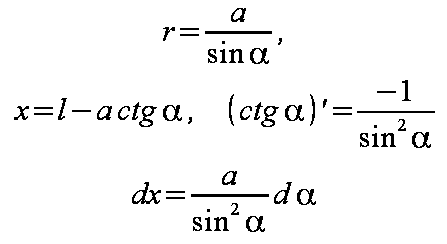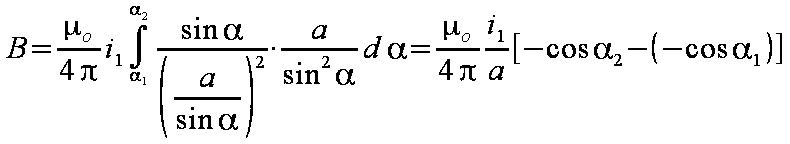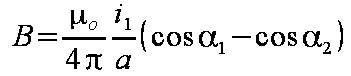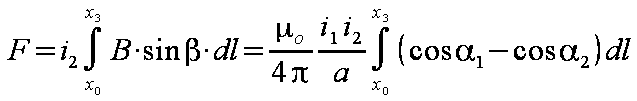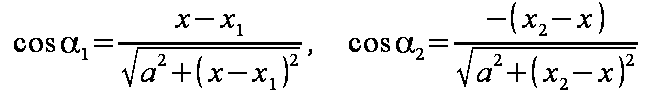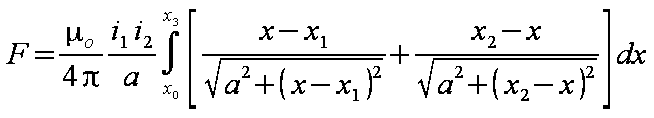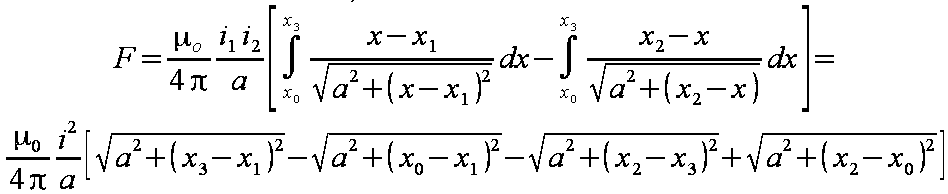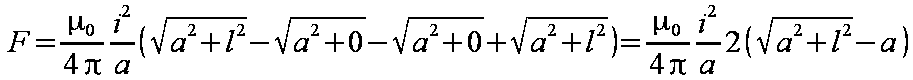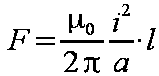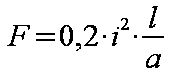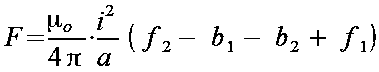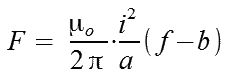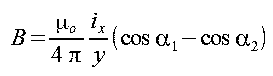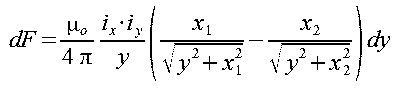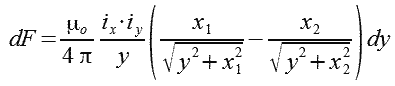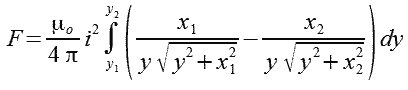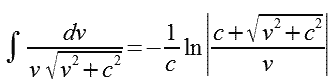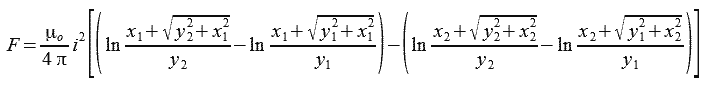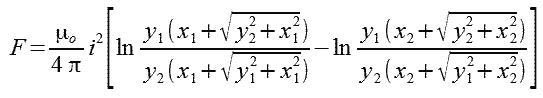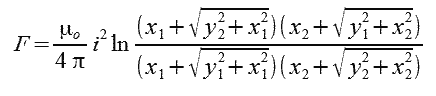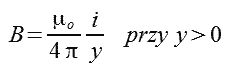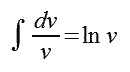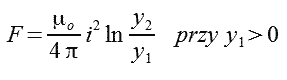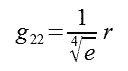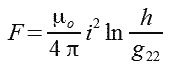1. Oddziaływanie elektrodynamiczne prostoliniowych torów prądowych równoległych

Do obliczeń sił oddziaływania elektrodynamicznego torów prądowych prostoliniowych wykorzystuje się równania Biota - Savarta, Ampera, Lorentza i Maxwella.

Jean Baptiste Biot_1774-1862		(1.1)	Felix Savart 1791-1841
Marie Ampere 1775-1836		(1.2)	Hendrik Antoon Lorentz 1853-1928
James_Clerk_Maxwell_1831-1879		(1.3)	Prawo Amperea uogólnione przez Maxwella: prąd i zmienne pole elektryczne tworzą wirowe pole magnetyczne.
	Oznaczenia: B - wektor indukcji magnetycznej; x - wektor elementu toru prądowego i1 wytwarzającego pole magnetyczne; l - wektor elementu toru prądowego i2, na który działa siła F; F - wektor siły; r - wektor odległości punktu w którym określana jest indukcja B; i1 - prąd w torze przewodzącym x; i2 - prąd w torze przewodzącym l; µo - przenikalność magnetyczna próżni µo= 4 π · 10-7 w H/m; j - wektor gęstości prądu; H - wektor natężenia pola magnetycznego; D - wektor indukcji elektrycznej; t - czas.

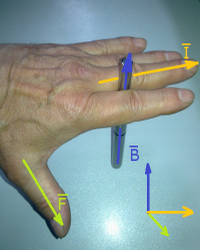
Sposoby wyznaczania kierunku oraz zwrotu wektorów indukcji i siły za pomocą dłoni i palców przedstawiono na fotografiach 1 - 4.

Fot. 1.

Fot. 2.

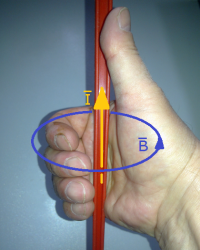
Fot. 3.

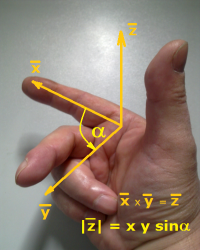
Fot. 4.

Obliczenia dla dwóch torów prądowych równoległych przeprowadzono w oparciu o poniższy rysunek pomocniczy.

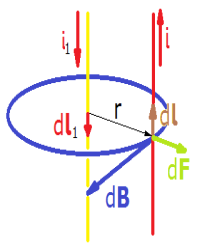
Rys. 1.1. Wyznaczanie kierunku siły

Rys. 1.2. Rysunek pomocniczy do obliczeń

Z równania Biota-Savarta (wzór 1.1) wyznacza się indukcję magnetyczną w punkcie P (rys. 1.2).

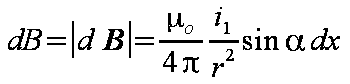	(1.4)

Całkowita indukcja B wymaga całkowania po całej długości toru x.

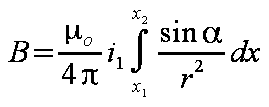	(1.5)

Po zamianie zmiennej x na zmienną α i wyrażeniu długości w kątach od α₁ do α₂ otrzymuje się równanie przedstawione wzorem 1.7.

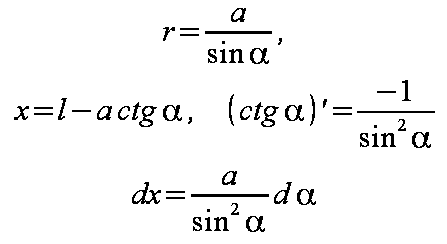	(1.6)

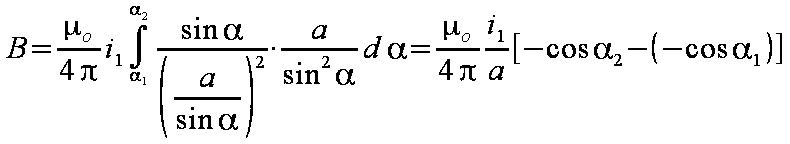	(1.7)

Wynik całkowania ujmuje wzór 1.8, który jest podstawą dalszych obliczeń siły.

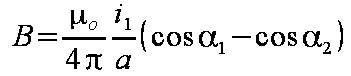	(1.8)

Po podstawieniu obliczonej indukcji B (wzór 1.8) do wzoru 1.2, otrzymuje się postać wyrażenia na siłę F jak we wzorze 1.9.

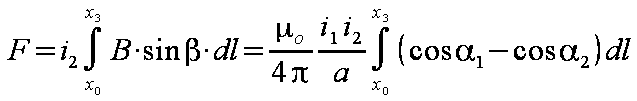	(1.9)

Tym razem wygodniej jest całkować względem zmiennej x, stąd zamiana funkcji kątowych na odpowiednie długości.

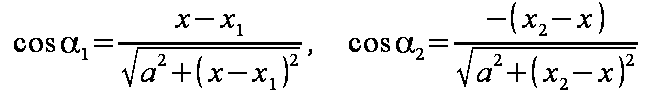	(1.10)

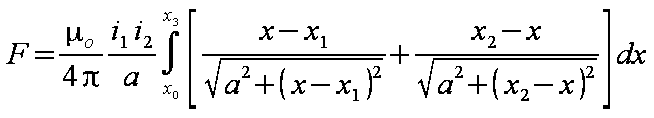	(1.11)

Wzór 1.12 pokazuje ogólne rozwiązanie całki, takiej jak otrzymana po podstawieniach (wzór 1.11).

	(1.12)

Ostatecznie rozwiązanie przyjmuje postać jak we wzorze 1.13. Dodatkowo można założyć, że prądy są jednakowe i₁=i₂=i.

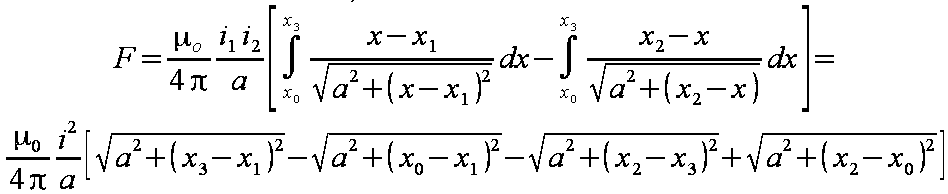	(1.13)

Jeśli przyjąć, że długości obydwu torów są równe i wynoszą l, tzn. x₁=x₀ oraz x₂=x₃, to wyrażenie uprości się do postaci wzoru 1.14.

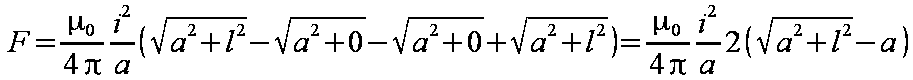	(1.14)

W przypadku, gdy l jest dużo większe od a (l>>a) wzór 1.14 przyjmie postać wzoru 1.15.

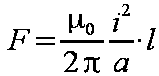	(1.15)

Po podstawieniu µ_o=4π · 10^-7 i prądu i w kA (10³) siła F wyrażona w niutonach może być obliczona z wzoru 1.16.

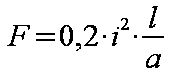	(1.16)

Jeśli do wzoru 1.13 wprowadzimy oznaczenia boków trapezu i przekątnych jak na rysunku 1.3 poniżej, to postać tego wyrażenia będzie łatwa do zapamiętania (wzór 1.17).

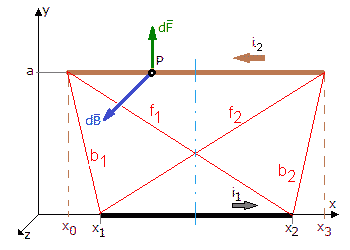
Rys. 1.3. Przekątne i boki trapezu opartego na torach prądowych

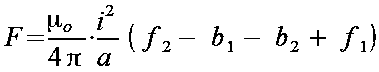	(1.17)

W przypadku, gdy przez środki obydwu torów równoległych o różnej długości można przeprowadzić oś symetrii (rys. 3), tzn.: f=f₁=f₂ oraz b=b₁=b₂, to równanie określające siłę przyjmie postać wzoru 1.18.

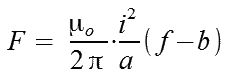	(1.18)

2. Oddziaływanie elektrodynamiczne prostoliniowych torów prądowych prostopadłych

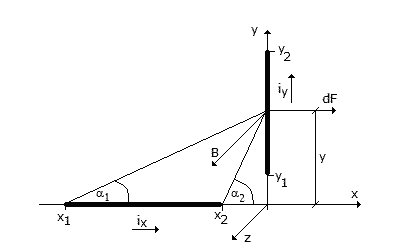
Rys. 2.1. Rozpatrywany model torów prądowych prostopadłych

W przypadku torów prostopadłych (rys. 2.1.), jeśli pominie się wpływ przekroju toru indukcja magnetyczna będzie określona wzorem 2.1. (patrz także wzór 1.8)

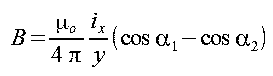	(2.1)

Po podstawieniu za cos α₁ i cos α₂ wymiarów z rysunku 2.1 otrzymuje się wzór 2.2.

	(2.2)

Siłę działającą na ramię y oblicza się z wzoru 2.3 (patrz wzór 1.9).

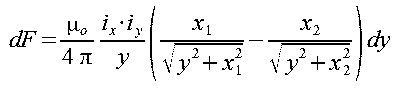	(2.3)

W punkcie oddalonym o y działa siła dF (rys. 2.1), której kierunek jest zgodny z osią x (wzór 2.4).

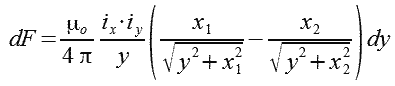	(2.4)

Całkowitą siłę działającą na prostopadły do osi x odcinek toru, otrzymuje się całkując na wzdłuż tego odcinka od y₁ do y₂ (wzór 2.5). W dalszych wzorach przyjęto, że prądy w obu odcinkach toru są równe i_x= i_y= i.

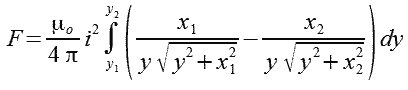	(2.5)

Całkę oblicza się korzystając z zależności 2.6,

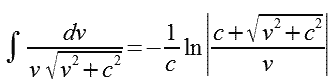	(2.6)

przy czym v (variable) oznacza zmienną, a c (constant) - stałą.

Najpierw po podstawieniu granic uzyskuje się postać przedstawioną wzorem 2.7:

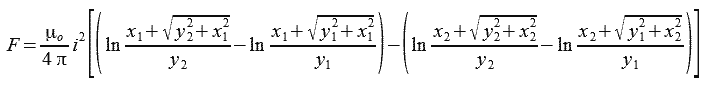	(2.7)

Po uproszczeniach zapisu uzyskuje się wzory 2.8 i ostatecznie 2.9.

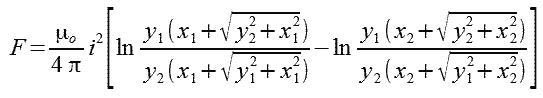	(2.8)

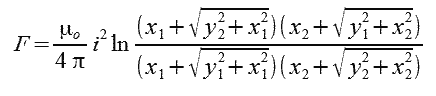	(2.9)

W przypadku gdy tor przebiegający wzdłuż osi x jest bardzo długi (x₁ → - ∞, a x₂= 0), wtedy cos(α₁)=1, a cos(alpha;₂)=0 i wzór 2.1 na indukcję uprości się do postaci 2.10.

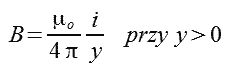	(2.10)

Natomiast siłę działającą na ramię mające kierunek osi y w prosty sposób można wyznaczyć wiedząc, że całka ogólna ma rozwiązanie jak we wzorze 2.11.

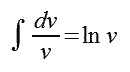	(2.11)

Ostatecznie siła ta jest określona wzorem 2.12.

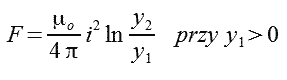	(2.12)

W rzeczywistych torach prądowych (rys. 2.2) należy uwzględnić średnią geometryczną odległość własną przewodu oznaczaną tu: g₂₂.

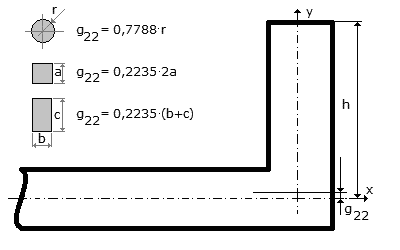
Rys. 2.2. Geometryczna odległość własna przewodu dla różnych przekrojów

Odległość ta zależy od przekroju toru prądowego. Przykładowo dla przekroju kołowego można ją obliczyć z zależności 2.13.

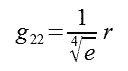	(2.13)

Dla przekroju prostokątnego posługujemy się wartością średnią geometryczną odległością własną przewodu lub wartościami dokładnymi zestawionymi w tablicy 2.1.

Ostateczny wzór na siłę działającą na rzeczywisty odcinek toru prądowego prostopadły do osi x można obliczyć z wzoru 2.14. Przy czym odcinek toru przebiegający wzdłuż osi x musi być znacznie dłuższy od h (rys. 2.2).

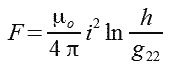	(2.14)

3. Oddziaływanie elektrodynamiczne prostoliniowych torów prądowych ukośnych

Zagadnienie wyznaczania sił w układach ukośnych przedstawiono na przykładzie, z którym można się zapoznać → TUTAJ .

Literatura

1. Kurdziel R., Działania cieplne i dynamiczne prądów zwarciowych, PWT Warszawa 1957
2. Au A., Ciok Zb., Aparaty elektryczne. Część I, WPW Warszawa 1975
3. Au A., Maksymiuk J., Pochanke Zb., Podstawy obliczeń aparatów elektroenergetycznych, WNT Warszawa 1982
4. Maksymiuk J., Pochanke Zb., Obliczenia i badania diagnostyczne aparatury rozdzielczej, WNT Warszawa 2001
5. Markiewicz H., Wołkowiński K., Urządzenia elektroenergetyczne, WNT Warszawa 1980
6. Markiewicz H., Urządzenia elektroenergetyczne, WNT Warszawa 2001
7. Baran K., Kutzner J., Zbiór zadań z podstaw elektroenergetyki, Wyd. Ucz. PWSZ Kalisz 2006