Purand
GEOMETRIA LICZB ZESPOLONYCH
Liczby zespolone przebijały się do świadomości uczonych ponad dwa wieki. Poczynając od Kartezjusza, który wprowadził deprecjonujące określenie "liczby urojone" w roku 1637, poprzez osiągnięcia takich matematyków jak J. Wallis (1616 - 1703), A. de Moivre (1667 - 1754), L. Euler (1707 - 1782) i in., aż do Carla F. Gaussa (1777 - 1855). W efekcie doceniono ich znaczenie w uproszczeniu rozwiązań wielu zagadnień głównie z dziedziny elektrotechniki.
W elektrotechnice symbol wielkości urojonych i, wprowadzony przez Eulera, jest powszechnie wykorzystywany do oznaczenia prądu elektrycznego, dlatego stosuje się oznaczenie części urojonej literą j. Jeśli używa się jednocześnie obydwu rodzajów liczb, to dla liczb zespolonych stosuje się podkreślenie ( z ), aby wyraźnie oznaczyć wielkości złożone z części rzeczywistej i części urojonej.

Liczby zespolone są reprezentowane przez punkty na płaszczyźnie zespolonej i mają ogólniejszy charakter niż liczby rzeczywiste. Liczby rzeczywiste są podzbiorem liczb zespolonych:

Na rysunku liczba zespolona jest reprezentowana przez punkt z, który można opisać różnymi postaciami wyrażeń matematycznych.
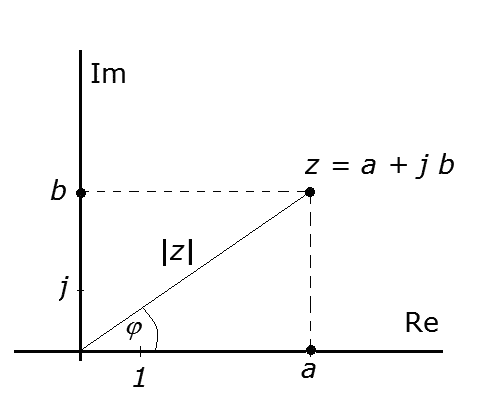
 | - postać algebraiczna |
 | - postać trygonometryczna, gdzie  jest modułem liczby zespolonej jest modułem liczby zespolonej |
 | - postać wykładnicza, w której wykorzystuje się wzór Eulera: z niego otrzymujemy z niego otrzymujemy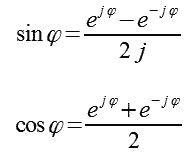 |
| Wzór Eulera można wyprowadzić rozpatrując rozwinięte w szeregi potęgowe funkcje wykładniczą dla liczb zespolonych i funkcje trygonometryczne sinus i cosinus: | |
 | |
|---|---|
Dodawanie liczb zespolonych można geometrycznie interpretować jako przesnięcie punktu 0 płaszczyzny do punktu z1 (płaszczyzna v" - h"), oznaczającego liczbę dodawaną.

Dodawanie liczb zespolonych z2 + z1

Odejmowanie to przesunięcie odwrotne.

Mnożenie przez z1 przeprowadza się przez skręcenie płaszczyzny zespolonej przeprowadzające oś h na z1 (płaszczyzna v'- h').


Mnożenie liczb zespolonych
Punkty po obrocie na rysunku oznaczono apostrofem np. 1 → 1', z1 → z1'. Kąt α jest stały dla odcinków równoległych np. 1-1' i z1 - (z1 x z1), co pozwala z twierdzenia Talesa wyznaczyć długość odcinka po wykonaniu mnożenia. Kierunek liczby zespolonej będącej wynikiem mnożenia wyznacza suma kątów ω+φ

Przykład:
Niech dana jednostka 1 ma długość 40 mm;
moduł z1=60 mm;
moduł z2=50 mm,
to z rysunku |z1 x z2|=75 mm.
Sprawdzenie: |z1|=60/40=1,5; |z2|=50/40=1,25; |z1 x z2|=75/40=1,875
|z1 x z2|= 1,5 x 1,25 = 1,875
Dzielenie, to skręcenie odwrotne z z1 na 1 (płaszczyzna v - h).

Na ostatnim rysunku pokazano sposób wyznaczania odwrotności liczby zespolonej z.

Wyznaczanie odwrotności liczby zespolonej z
Po obrocie płaszczyzny zgodnie z ruchem wskazówek zegara o kąt φ uzyskuje się punkty z' i 1'. Odcinek równoległy do prostej łączącej te punkty z punktu 1 wyznacza szukane położenie punktu 1/z.